Problem:

You are given an array target of n integers. From a starting array arr consisting of n 1's, you may perform the following procedure :

• let x be the sum of all elements currently in your array.
• choose index i, such that 0 <= i < n and set the value of arr at index i to x.
• You may repeat this procedure as many times as needed.

Return true if it is possible to construct the target array from arr, otherwise, return false.

Example 1:
Input: target = [9,3,5]
Output: true
Explanation: Start with arr = [1, 1, 1] [1, 1, 1], sum = 3 choose index 1 [1, 3, 1], sum = 5 choose index 2 [1, 3, 5], sum = 9 choose index 0 [9, 3, 5] Done

Example 2:
Input: target = [1,1,1,2]
Output: false
Explanation: Impossible to create target array from [1,1,1,1].

Example 3:
Input: target = [8,5]
Output: true

Constraints:

• n == target.length
• 1 <= n <= 5 * 104
• 1 <= target[i] <= 109

Solution:

Using Max-Heap:

Algorithm: The best approach to this question can be obtained by realising that it's quite time-consuming to start with our ones array and try to get to target. This is because there are just too many possibilities that we could branch into since it isn't clear what indexes need to be replaced.

Therefore, since we're already given the final result after each operation, we can just start with that and see if it's possible to reach our ones array going backwards.

---

Logic:

So, where should we start? Well, we know that each new number is going to be larger than the previous. Therefore, we will start with the largest number and try and find what used to be there before adding it.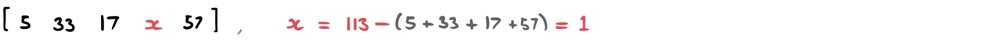

If we let x be the number that used to be there, we know we can retrieve x since we know what the previous sum must have been: 113; We were only able to add 113 because that was the previous sum. Therefore x = prevSum - (everything else).

Let's continue this frame of thought with the rest of the array, picking the largest number each time: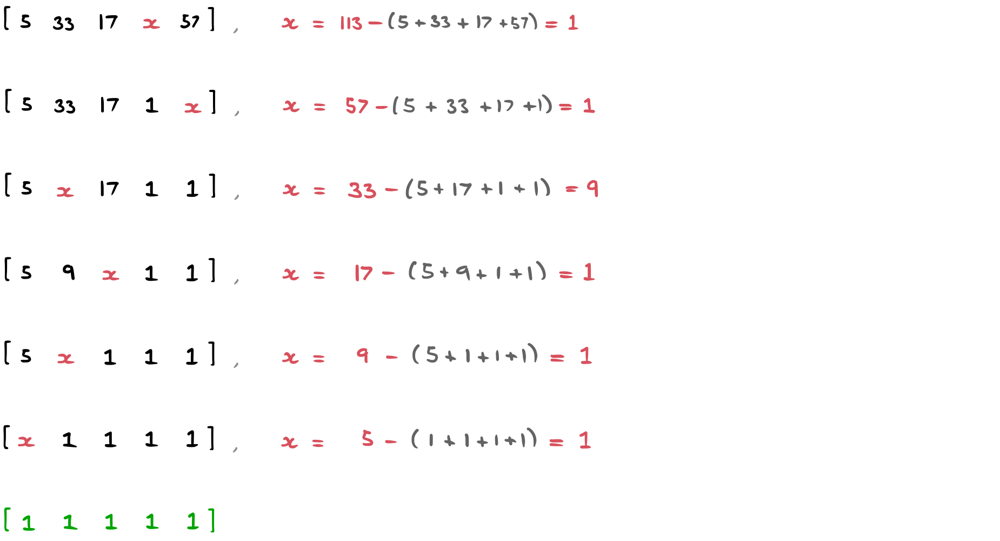

Awesome! That's basically how our algorithm will work.

If we are never able to reach a row of ones, we return false.

---

Major optimisation:

The above procedure works quite well but is inefficient in a particular situation. Imagine if we had an array where one number is much larger than the others. That implies that the same sum has been added to that number multiple times. Observe the following example: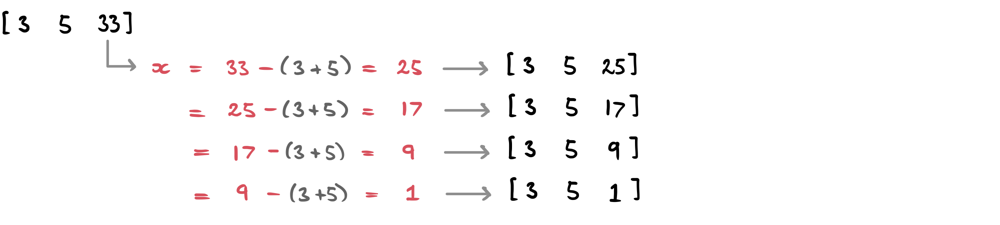

As you can see, we continuously subtract (3+5) from our largest number. The way we avoid all this repetitive work is by simply taking the modulus:

If we keep subtracting the same value from our number, we're effectively finding what the remainder would be once it's no longer the largest number.

---

How would this work in code?

It's actually quite simple! We need the largest number each time, so we can just put all our numbers in a max-heap. In the below, assume curr represents the current largest number.

• To get x, we can simply do x = curr % (sum - curr) since sum - curr represents the sum of all numbers in the array except the current max.
• Once we have x, we'll update sum to sum - curr + x to get our new sum.
• Before adding x to the priority queue, we need to check a couple of things:
  • If x == 0, that implies it was impossible to get to this point with an array of ones. We return false.
  • If x == curr, that implies our modulus operator did not change our value. We return false.
• We return true once our priority queue only has 1s in it.

We also need to account for a couple special cases:

• If n == 1, we can return true if target[0] == 1. Otherwise, return false.
• In our while-loop, if n == 2, we return true if sum - curr == 1 which only happens when n == 2.

class Solution {
    public boolean isPossible(int[] target) {
        if (target.length == 1) return target[0] == 1;

        PriorityQueue<Integer> maxHeap = new PriorityQueue<>((a, b) -> b - a);
        int sum = 0;
        for(int num: target) {
            sum += num;
            maxHeap.offer(num);
        }

        while(maxHeap.peek() != 1) {
            int curr = maxHeap.poll();
            if (sum - curr == 1) return true;
            int x = curr % (sum - curr); // equivalent of doing curr - (sum - curr) repeatedly
            if (x == 0 || x == curr) return false;

            sum = sum - curr + x;
            maxHeap.offer(x);
        }
        return true;
    }
}

Time Complexity: O(nlogn) due to the priority queue.
Space Complexity: O(n) for using priority queue

Reference:

• Leetcode discussion